Sensor Signal Conditioning

Typically a sensor cannot be directly connected to the instruments that record, monitor, or process its signal, because the signal may be incompatible or may be too weak and/or noisy. The signal must be conditioned—i.e., cleaned up, amplified, and put into a compatible format.

Resistive elements are some of the most common sensors. They are inexpensive to manufacture and relatively easy to interface with signal conditioning circuits. Resistive elements can be made sensitive to temperature, strain (by pressure or by flex), and light. Using these basic elements, many complex physical phenomena can be measured, such as fluid or mass flow (by sensing the temperature difference between two calibrated resistances) and dew-point humidity (by measuring two different temperature points), etc. Bridge circuits are often incorporated into force, pressure and acceleration sensors.

Sensor elements’ resistances can range from less than 100 Ω to several hundred kΩ, depending on the sensor design and the physical environment to be measured. For example, RTDs (resistance temperature devices) are typically 100 Ω or 1000 Ω. Thermistors are typically 3500 Ω or higher.

Bridge Circuits

Resistive sensors such as RTDs and strain gages produce small percentage changes in resistance in response to a change in a physical variable such as temperature or force. Platinum RTDs have a temperature coefficient of about 0.385%/°C. Thus, in order to accurately resolve temperature to 1°C, the measurement accuracy must be much better  than 0.385 Ω, for a 100 Ω RTD.

Strain gages present a significant measurement challenge because the typical change in resistance over the entire operating range of a strain gage may be less than 1% of the nominal resistance value. Accurately measuring small resistance changes is therefore critical when applying resistive sensors.

Bridges offer an attractive alternative for measuring small resistance changes accurately. The basic Wheatstone bridge (actually developed by S. H. Christie in 1833) is shown in Figure 1. It consists of four resistors connected to form a quadrilateral, a source of excitation (voltage or current) connected across one of the diagonals, and a voltage detector connected across the other diagonal. The detector measures the difference  between the outputs of two voltage dividers connected across the excitation.

Fig 1. The Wheatstone bridge

A bridge measures resistance indirectly by comparison with a similar resistance. The two principal ways of operating a bridge are as a null detector or as a device that reads a difference directly as voltage.

When R1/R4 = R2/R3, the resistance bridge is at a null, regardless of the mode of excitation (current or voltage, AC or DC), the magnitude of excitation, the mode of readout (current or voltage), or the impedance of the detector. Therefore, if the ratio of R2/R3 is fixed at K, a null is achieved when R1 = K·R4. If R1 is unknown and R4 is an accurately determined variable resistance, the magnitude of R1 can be found by adjusting R4 until null is achieved. Conversely, in sensor-type measurements, R4 may be a fixed reference, and a null occurs when the magnitude of the external variable (strain, temperature, etc.) is such that R1 = K·R4.

Null measurements are principally used in feedback systems involving electrome-chanical and/or human elements. Such systems seek to force the active element (strain gage, RTD, thermistor, etc.) to balance the bridge by influencing the parameter being measured. For the majority of sensor applications employing bridges, however, the deviation of one or more resistors in a bridge from an initial value is measured as an indication of the magnitude (or a change) in the measured variable. In this case, the output voltage change is an indication of the resistance change. Because very small resistance changes are common, the output voltage change may be as small as tens of millivolts, even with VB = 10 V (a typical excitation voltage for a load cell application).

Constant Voltage Excitation Bridge

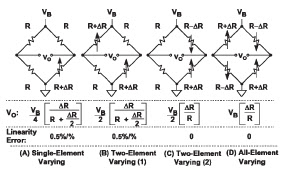
In many bridge applications, there may be two, or even four, elements that vary. Figure 2 shows four commonly used bridges suitable for sensor applications and the corresponding equations which relate the bridge output voltage to the excitation voltage and the bridge resistance values. In this case, we assume a constant voltage drive, VB. Note that since the bridge output is directly proportional to VB, the measurement accuracy can be no better than that of the accuracy of the excitation. .

Fig 2. Output voltage and linearity error
voltage for constant voltage drive bridge configurations

In each case, the value of the fixed bridge resistor, R, is chosen to be equal to the nominal value of the variable resistor(s). The deviation of the variable resistor(s) about the nominal value is proportional to the quantity being measured, such as strain (in the case of a strain gage) or temperature (in the case of an RTD).

The sensitivity of a bridge is the ratio of the maximum expected change in the output voltage to the excitation voltage. For instance, if VB = 10 V, and the full-scale bridge output is 10 mV, then the sensitivity is 1 mV/V.

The single-element varying bridge is most suited for temperature sensing using RTDs or thermistors. This configuration is also used with a single resistive strain gage. All the resistances are nominally equal, but one of them (the sensor) is variable by an amount ∆R. As the equation indicates, the relationship between the bridge output and ∆R is not linear. 

For example, if R = 100 Ω, and ∆R = 0.152, (0.1% change in resistance), the output of the bridge is 2.49875 mV for VB = 10 V. The error is 2.50000 mV – 2.49875 mV, or 0.00125 mV. Converting this to a percent of full scale by dividing by 2.5 mV yields an end-point linearity error in percent of approximately 0.05%. (Bridge end-point linearity error is calculated as the worst error in % FS from a straight line which connects the origin and the end point at FS, i.e. the FS gain error is not included). 

If ∆R = 1 Ω (1% change in resistance), the output of the bridge is 24.8756 mV, representing an end-point linearity error of approximately 0.5%. The end-point linearity error of the single-element bridge can be expressed in equation form:

Single-Element Varying Bridge End-Point Linearity Error ≈ % Change in Resistance ÷ 2
 

It should be noted that the above nonlinearity refers to the nonlinearity of the bridge itself and not the sensor. In practice, most sensors exhibit a certain amount of their own nonlinearity which must be accounted for in the final measurement.

In some applications, the bridge nonlinearity may be acceptable, but there are various methods available to linearize bridges. Since there is a fixed relationship between the bridge resistance change and its output (shown in the equations), software can be used to remove the linearity error in digital systems. Circuit techniques can also be used to linearize the bridge output directly, and these will be discussed shortly.

There are two possibilities to consider in the case of the two-element varying bridge. In the first, Case (1), both elements change in the same direction, such as two identical strain gages mounted adjacent to each other with their axes in parallel. The nonlinearity is the same as that of the single-element varying bridge, however the gain is twice that of the single-element varying bridge. The two-element varying bridge is commonly found in pressure sensors and flow meter systems. 

A second configuration of the two-element varying bridge, Case (2), requires two identical elements that vary in opposite directions. This could correspond to two identical strain gages: one mounted on top of a flexing surface, and one on the bottom. Note that this configuration is linear, and like two-element Case (1), has twice the gain of the single-element configuration. 

Another way to view this configuration is to consider the terms R + ∆R and R – ∆R as comprising the two sections of a centertapped potentiometer. The all-element varying bridge produces the most signal for a given resistance change and is inherently linear. It is an industry-standard configuration for load cells which are constructed from four identical strain gages.

Constant Current Excitation Bridge

Bridges may also be driven from constant current sources as shown in Figure 3. Current drive, although not as popular as voltage drive, has an advantage when the bridge is located remotely from the source of excitation because the wiring resistance does not introduce errors in the measurement. Note also that with constant current excitation, all configurations are linear with the exception of the single-element varying case.

Figure 3. Output voltage and linearity error 

for constant current drive bridge configurations

In summary, there are many design issues relating to bridge circuits. After selecting the basic configuration, the excitation method must be determined. The value of the excitation voltage or current must first be determined. Recall that the full scale bridge output is directly proportional to the excitation voltage (or current). 

Typical bridge sensitivities are 1 mV/V to 10 mV/V. Although large excitation voltages yield proportionally larger full scale output voltages, they also result in higher power dissipation and the possibility of sensor resistor self-heating errors. On the other hand, low values of excitation voltage require more gain in the conditioning circuits and increase the sensitivity to noise.

Regardless of its value, the stability of the excitation voltage or current directly affects the overall accuracy of the bridge output. Stable references and/or ratiometric techniques are required to maintain desired accuracy.

Bridge considerations

• Selecting Configuration (1,2,4 - Element Varying)
• Selection of Voltage or Current Excitation
• Stability of Excitation Voltage or Current
• Bridge Sensitivity: FS Output / Excitation Voltage, 1mV / V to 10mV / V Typical
• Fulscale Bridge Outputs: 10mV - 100mV Typical
• Precission Low Noise Amplification / Conditioning Techniques Required
• Linearization Techniques May Be Required
• Remote Sensors Present Challenges.

Handbook Of Sensor, Transducer, Actuator,MEMS, Nano Technology, etc. : Sensor & Transducer Store