Ultrasonic sensing techniques have become mature and are widely used in the various fields of engineering and basic science. Actually, many types of conventional ultrasonic instruments, devices and sophisticated software are commercialized and used for both industrial and medical applications. One of advantages of ultrasonic sensing is its outstanding capability to probe inside objectives nondestructively because ultrasound can propagate through any kinds of media including solids, liquids and gases except vacua.
In typical ultrasonic sensing the ultrasonic waves are travelling in a medium and often focused on evaluating objects so that a useful information on the interaction of ultrasonic energy with the objects are acquired as ultrasonic signals that are the wave forms variations with transit time. Such ultrasonic data provides the fundamental basis for describing the outputs of ultrasonic sensing and evaluating systems.
In typical ultrasonic sensing the ultrasonic waves are travelling in a medium and often focused on evaluating objects so that a useful information on the interaction of ultrasonic energy with the objects are acquired as ultrasonic signals that are the wave forms variations with transit time. Such ultrasonic data provides the fundamental basis for describing the outputs of ultrasonic sensing and evaluating systems.
Features of Ultrasonic Waves
Ultrasound is an acoustic wave with a frequency higher than the audible range of the human ear, which is 20 kHz. Ultrasound can be within the audible range for some animals, like dogs, bats, or dolphins. In the years around 1883, Sir Francis Galton performed the first known experiments with whistles generating ultrasound. Many decades later, people started to find ultrasound applications in engineering, medicine, and daily life.
The basic principle for the use of ultrasound as a measurement tool is the time-of-flight technique. The pulse-echo method is one example. In the pulse-echo method, a pulse of ultrasound is transmitted in a medium. When the pulse reaches an another medium, it is totally or partially reflected, and the elapsed time from emission to detection of the reflected pulse is measured. This time depends on the distance and the velocity of the sound. When sound travels with a known velocity c, the time t elapsed between the outgoing signal and its incoming echo is a measure of the distance d to the object causing the echo.
The basic principle for the use of ultrasound as a measurement tool is the time-of-flight technique. The pulse-echo method is one example. In the pulse-echo method, a pulse of ultrasound is transmitted in a medium. When the pulse reaches an another medium, it is totally or partially reflected, and the elapsed time from emission to detection of the reflected pulse is measured. This time depends on the distance and the velocity of the sound. When sound travels with a known velocity c, the time t elapsed between the outgoing signal and its incoming echo is a measure of the distance d to the object causing the echo.
It is known that frequency range of sound audible to humans is approximately 20–20,000Hz (cycles per second). Ultrasound is simply sound that are above the frequency range of human hearing. When a disturbance occurs at a portion in an elastic medium, it propagates through the medium in a finite time as a mechanical sound wave by the vibrations of molecules, atoms or any particles present. Such mechanical waves are also called elastic waves. Ultrasound waves or ultrasonic waves are the terms used to describe elastic waves with frequency greater than 20,000Hz and normally exist in solids, liquids, and gases.
It is important to understand the behaviour and properties of ultrasonic waves in media, to design ultrasonic sensors and develop ultrasonic sensing systems. Some basic features of ultrasonic waves are introduced here.
Types of Wave (Modes of Propagation)
What types of ultrasonic waves can exist? The answer to this question can basically be given from solutions of the wave equations that predict wave behaviours by showing that material properties and body shape dictate the vibrational response to the applied forces that drive the wave motion. In short, there are two types of ultrasonic waves: bulk (fundamental) waves that propagate inside of anobject, and guided waves that propagate near the surface or along the interface of an object.
Waves that propagate wholly inside an object, independent of its boundary and shape, are called bulk waves. Two types of bulk waves can exist in an isotropic medium: longitudinal (or dilatational, compression, primary), and shear (or distortional, transverse, secondary) waves as shown schematically in Fig. 1.
Ultrasonic wave propagations are usually described in terms of the direction of particles motion in relation to the direction in which the wave propagates. The longitudinal waves can be defined on this basis as waves in which the particle motion is parallel to the direction of the wave propagation.
The shear waves are defined as waves in which the particle motion is perpendicular to the direction of the propagation. Both waves can exist in solids because solids, unlike liquids and gasses, have rigidity that is a resistance to shear aswell as compressive loads. However, the shear waves cannot exist in liquids and gasses because of no resistance to shear roads in such media.
When the influences of the boundaries or shape of an object are considered, other types of waves called the guided waves are produced. There are three types of guided waves depending on geometry of an object: surface acoustic waves (SAWs), plate waves, and rod waves. SAWs are defined as waves that propagate along a free surface, with disturbance amplitude that decays exponentially with depth into the object.
There are many kinds of SAWs such as Rayleigh, Scholte, Stoneley, and Love waves and the wave propagation characteristics of SAWs strongly depend on material properties, surface structure, and nature at the interface of the object. When an SAW propagates along a boundary between a semi-infinite solid and air, the wave is often called Rayleigh wave in which the particle motion is elliptical and the effective penetration depth is of the order of one wavelength. Among many types of SAWs, Rayleigh wave is the most common and well-known wave so that many researchers often call any SAWs Rayleigh wave.
When an ultrasonic wave propagates in a finite medium (like a plate), the wave is bounded within the medium and may resonate. Such waves in an object of finite size are called plate waves if the object has a multilayer structure, and called Lamb waves if it has a single layer. Also, when a force is applied to the end of a slender rod, an ultrasonic wave propagates axially along it.
In general, the wave propagation characteristics of guided waves Ultrasonic strongly depend on not only material properties but also the plate thickness, the rod diameter, and the frequency. The frequency dependence of the wave velocity of guided waves is called frequency dispersion. While the frequency dispersion often makes wave propagation behaviour complicated, it also provides unique materials evaluations using guided waves. It is noted that similar types of bulk and guided waves can exist for anisotropic materials and in general, their behaviours become much more complicated than those for isotropic materials.
Velocity
Ultrasonic velocity is probably the most important and widely used parameter in ultrasonic sensing applications. Each medium has its own value of the velocity that usually depends on not only propagation medium but also its geometrical shape and structure. The theoretical values can be obtained from wave equations and typically determined by the elastic properties and density of the medium. For example, the wave equations for an isotropic solid give the following simple formulae for the longitudinal and shear wave velocities:
 here, vl and vs are the longitudinal and shear wave velocities, respectively, E is Young’s modulus, v is Poisson’s ratio, G is shear modulus and ρ is the density. For most of solid materials the longitudinal wave velocity is faster than the shear wave velocity because the shear modulus is lower than the Young’s modulus. It is noted that Poisson’s ratio is not a dominant factor affecting the velocities. As a rule of thumb, the velocity of the shear wave is roughly half the longitudinal wave.
here, vl and vs are the longitudinal and shear wave velocities, respectively, E is Young’s modulus, v is Poisson’s ratio, G is shear modulus and ρ is the density. For most of solid materials the longitudinal wave velocity is faster than the shear wave velocity because the shear modulus is lower than the Young’s modulus. It is noted that Poisson’s ratio is not a dominant factor affecting the velocities. As a rule of thumb, the velocity of the shear wave is roughly half the longitudinal wave.Although the velocities can be determined theoretically if material properties such as the elastic moduli and density are known precisely, these material properties are not always available for the determination because they change depending on mechanical processing and heat treatments. Therefore, it is important and necessary tomake a calibration measurement for the velocities when one wants to know the correct values for velocities.
Attenuation
When an ultrasonic wave propagates through a medium, ultrasonic attenuation is caused by a loss of energy in the ultrasonic wave and other reasons. The attenuation can be seen as a reduction of amplitude of the wave. There are some factors affecting the amplitude and waveform of the ultrasonic wave, such as ultrasonic beam spreading, energy absorption, dispersion, nonlinearity, transmission at interfaces, scattering by inclusions and defects, Doppler effect and so on. To characterize the ultrasonic attenuation quantitatively, attenuation coefficient α is defined as follows:
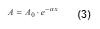
where A is the peak amplitude of the wave at propagation distance x, A0 is the initial peak amplitude.The attenuation coefficient α is experimentally determined from the variation of the peak amplitude with the propagation distance, and it can be given in decibel per metre (dB/m) or in neper per metre (Np/m). In general, the attenuation coefficient highly depends on frequency. Since this frequency dependence reflects microstructures of materials, it can be used for characterizing microscopic material properties relating to chemical reactions and mechanical processes.
Wavelength λ is the distance over which one spatial cycle of the wave completes and the following expression can be given,

where v is the ultrasonic velocity and f is the frequency. Wavelength is a useful parameter in ultrasonic sensing and evaluations. In ultrasonic detection of a small object, the smallest size that can clearly be detected must be larger than half a wavelength at the operating frequency. If the critical size of an object to be detected is known, such prior information on size is helpful for selecting an appropriate frequency for measurements.
When an ultrasonic wave perpendicularly impinges on an interface between two
media as shown in Fig. 2, a part of the wave is reflected back to the medium 1 and the remainder is transmitted to the medium 2.

The ratio of the amplitude of the reflected wave AR to that of the incident wave AI is called reflection coefficient R, and the ratio of the amplitude of the transmitted wave AT to that of the AI is called transmission coefficient T. Considering a balance of stresses and a continuity of velocities on both sides of the interface, the reflection and transmission coefficients, R and T can be given as follows:

where subscripts 1 and 2 refer to the medium 1 and 2, respectively, and z is the acoustic impedance defined as (1). It can be seen from these equations that the maximum transmission of ultrasonic wave occurs when the impedances of the two media are identical, and most of ultrasonic wave is reflected when the two media have very different impedances. The reflection and transmission at interface play an important role in designing ultrasonic sensing systems and understanding experimental results with the ultrasonic systems.
When an ultrasonic wave obliquely impinges on an interface between two media as shown in Fig. 3, several things happen depending on the incident angle of the wave as well as the material properties of the two media. One of important things is refraction in which a transmitted wave has a different angle from the incident. The refraction is basically caused by the velocity difference on either side of the interface. The refraction angle can be calculated from Snell’s law if the velocities of the two media and the incidence angle are known.
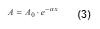
where A is the peak amplitude of the wave at propagation distance x, A0 is the initial peak amplitude.The attenuation coefficient α is experimentally determined from the variation of the peak amplitude with the propagation distance, and it can be given in decibel per metre (dB/m) or in neper per metre (Np/m). In general, the attenuation coefficient highly depends on frequency. Since this frequency dependence reflects microstructures of materials, it can be used for characterizing microscopic material properties relating to chemical reactions and mechanical processes.
Wavelength
Wavelength λ is the distance over which one spatial cycle of the wave completes and the following expression can be given,

where v is the ultrasonic velocity and f is the frequency. Wavelength is a useful parameter in ultrasonic sensing and evaluations. In ultrasonic detection of a small object, the smallest size that can clearly be detected must be larger than half a wavelength at the operating frequency. If the critical size of an object to be detected is known, such prior information on size is helpful for selecting an appropriate frequency for measurements.
Reflection and Transmission
When an ultrasonic wave perpendicularly impinges on an interface between two
media as shown in Fig. 2, a part of the wave is reflected back to the medium 1 and the remainder is transmitted to the medium 2.

The ratio of the amplitude of the reflected wave AR to that of the incident wave AI is called reflection coefficient R, and the ratio of the amplitude of the transmitted wave AT to that of the AI is called transmission coefficient T. Considering a balance of stresses and a continuity of velocities on both sides of the interface, the reflection and transmission coefficients, R and T can be given as follows:

where subscripts 1 and 2 refer to the medium 1 and 2, respectively, and z is the acoustic impedance defined as (1). It can be seen from these equations that the maximum transmission of ultrasonic wave occurs when the impedances of the two media are identical, and most of ultrasonic wave is reflected when the two media have very different impedances. The reflection and transmission at interface play an important role in designing ultrasonic sensing systems and understanding experimental results with the ultrasonic systems.
Refraction and Mode Conversion

Another important phenomenon is mode conversion that is a generation of one type of wave from another type in refraction as shown in Fig. 3. For example, a longitudinal wave incident on an interface between liquid and solid is transmitted partially as a refracted longitudinal wave and partially as a mode converted shear wave in the solid. Mode conversion can also take place on reflection if the liquid shown in Fig. 3 is a solid. It is noted that any types of waves can be converted to another type, e.g. from a shear wave to a longitudinal wave, and from a longitudinal wave to a surface wave. The angles of reflection and/or refraction by mode conversion can be calculated fromSnell’s law.
Figure 4 shows a simulation result for refraction and mode conversion, calculated by a finite difference method. We can see that an incident plane wave (longitudinal wave) of 10◦ in water is refracted at the refraction angle of 43◦ in steel and simultaneously converted to shear wave at refraction angle of 22◦.

Ultrasonic Reference:
 |
| Wave Motion in Elastic Solids |
 |
| Piezoelectric and Acoustic Mater... |
Can't find what you looking for? Please search in the web here:
Custom Search
Applications of Ultrasound







3 comments:
Nice post..thanks for share..
February 19, 2011 at 6:33 AMhow nice
February 24, 2011 at 12:18 AMnice post
February 24, 2011 at 12:22 AMPost a Comment